Giới thiệu về cấu trúc Heap. Ví dụ minh họa

Để hiểu rõ hơn về kiểu dữ liệu ở dạng bộ sưu tập, nội dung bài viết dưới đây FUNiX sẽ giới thiệu về cấu trúc Heap để bạn tham khảo và ứng dụng cho việc lập trình.

>> Khóa học lập trình cơ bản

>> Lập trình hướng đối tượng (bằng Java)

Khi biểu diễn dữ liệu ở dạng bộ sưu tập (collection), ngoài việc sử dụng các kiểu dữ liệu như danh sách (list), tập hợp (set), khóa – giá trị (dictionary) hay hàng đợi (queue), bạn có thể dùng thêm Heap.

1. Giới thiệu về cấu trúc Heap

Heap là loại cấu trúc dữ liệu dạng cây và các node trong cây đó được sắp xếp theo một thứ tự nhất định, có thể là theo chiều tăng dần hoặc giảm dần.

Cấu trúc Heap là một dạng của cấu trúc dữ liệu cây nhị phân cân bằng. Trong đó, khóa của nút gốc được so sánh với các con của nó theo một trình tự phù hợp. 

Khi tổng giá trị của nút cha lớn hơn hoặc bằng tổng giá trị của nút con, thì thuộc tính này tạo ra một Max Heap. Còn nếu tổng giá trị nút cha nhỏ hơn hoặc bằng tổng giá trị của nút con thì thuộc tính này tạo ra một Min Heap.

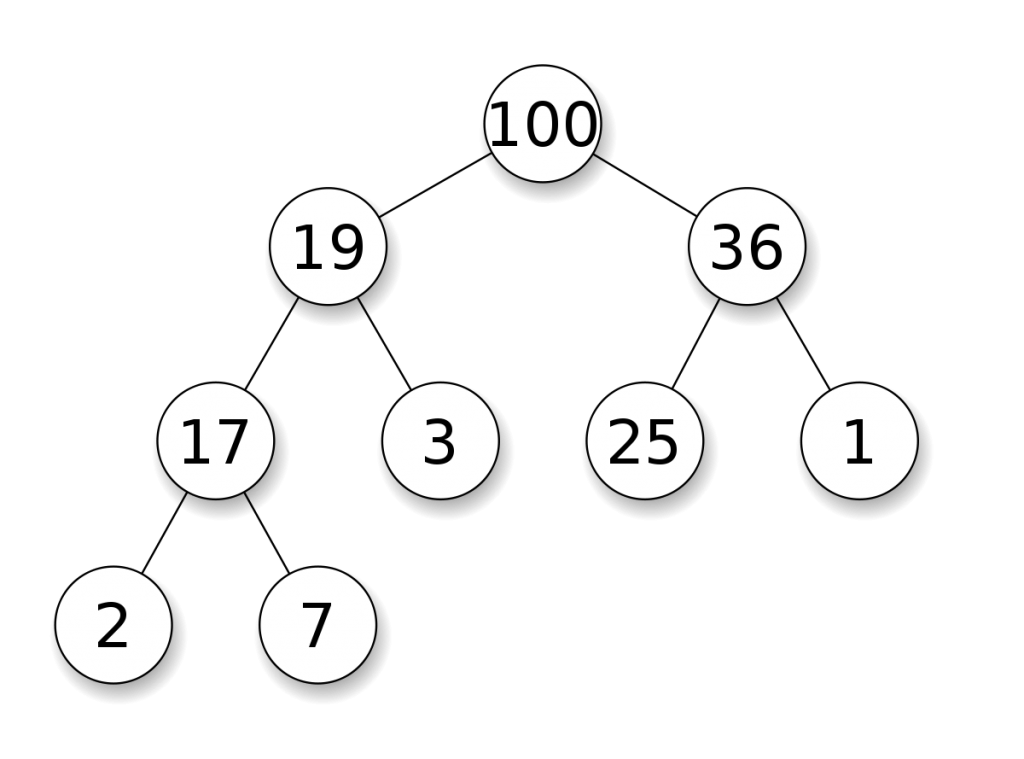
Các thao tác thường gặp trên Heap:

• Tìm max (tìm min): Tìm khóa lớn nhất trong max-heap (tìm khóa nhỏ nhất trong đống-min). Thời gian thực hiện phép toán trên đống nhị phân là O(1).
• Xóa max (xóa min): Xóa nút gốc của max-heap (min-heap). Thời gian thực hiện là O(log n).
• Tăng khóa (giảm khóa): Thay đổi giá trị một khóa trong max-heap (min-heap). Thời gian thực hiện là O(log n).
• Chèn: Chèn thêm một khóa mới vào đống. Thời gian thực hiện là O(log n).
• Hợp: Hợp hai Heap lại thành một Heap mới chứa tất cả các khóa của cả hai. Thời gian thực hiện là O(n).

Cấu trúc Heap được sử dụng khi phần tử có thứ tự, ưu tiên cao nhất hoặc thấp nhất cần được loại bỏ. Chúng cho phép bạn truy cập nhanh mục này trong thời gian O (1). Thêm một công dụng hữu ích nữa của heap là triển khai hàng đợi ưu tiên.

Bên cạnh đó, các đống nhị phân thường được triển khai bằng cách sử dụng mảng. Việc này giúp tiết kiệm chi phí lưu trữ con trỏ đến các nút con.

2. Ví dụ minh họa về cấu trúc Heap

Ví dụ về cấu trúc Heap: Ta có một Heap chứa 7 node và giá trị các node nhựa sau: {6, 4, 5, 3, 2, 0, 1}.

Theo đó, bạn có thể dùng một mảng để chứa giá trị các node của một Heap theo cách được mô tả trong hình sau:

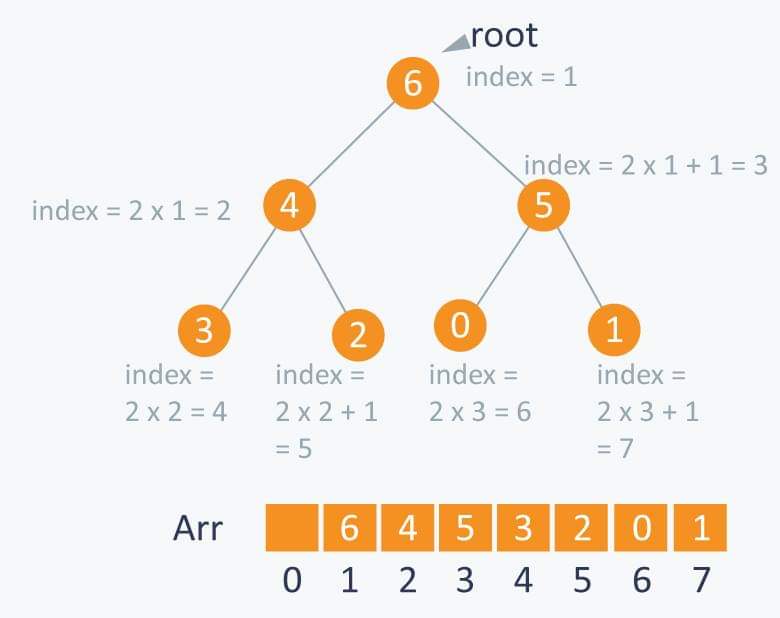
Như vậy, nếu ta lưu một phần tử của heap ở vị trí có chỉ số i trong mảng A thì:

• Node cha của nó sẽ được lưu ở vị trí có chỉ số là i/2, trừ khi node đó là root, vì root không có cha.
• Node con bên trái của nó sẽ được lưu ở vị trí có chỉ số là i*2, node con bên phải được lưu ở vị trí i*2 + 1.
• Vị trí số 1 được lưu luôn là Node root.

Một số thao tác thường dùng trong xử lý Heap:

• Upheap: Khi có một nút lớn hơn cha của nó thì di chuyển nó lên trên.
• Down Heap: Khi có một phần tử nhỏ hơn một con của nó thì di chuyển xuống dưới.
• Push: Đưa 1 phần tử vào Heap bằng cách thêm 1 nút vào cây và upheap nút đó.
• Del: Loại 1 phần tử khỏi Heap bằng cách chuyển nó xuống cuối heap và loại bỏ, sau đó chỉnh sửa lại heap sao cho thoả mãn các điều kiện của Heap.

Heap được sử dụng trong thuật toán Dijkstra, Kruskal, Heap Sort nhằm giảm độ phức tạp thuật toán. Đặc biệt, heap còn có thể sử dụng trong các bài toán dãy số, QHĐ, đồ thị… Qua những ví dụ trên, chúng ta có thể thấy được sự đa dạng và linh hoạt trong việc sử dụng cấu trúc Heap.

Nhìn chung, mỗi thủ tục của Heap có độ phức tạp không quá O(logn). Vì vậy, Heap giúp giải quyết các bài toán một cách đơn giản, trong thời gian cho phép. Mong rằng, nội dung bài viết giới thiệu về cấu trúc Heap của FUNiX trên đây sẽ giúp ích cho bạn trong việc lập trình!

Phạm Thị Thanh Ngọc