Hướng dẫn giải 1 số bài toán tìm đường đi ngắn nhất và tô màu trên đồ thị trong cấu trúc dữ liệu và giải thuật

Trong bài viết dưới đây, FUNiX sẽ hướng dẫn bạn giải 1 số bài toán tìm đường đi ngắn nhất và tô màu trên đồ thị trong cấu trúc dữ liệu và giải thuật. Các bạn sinh viên ngành công nghệ thông tin nếu đang quan tâm đến nội dung kiến thức này, thì đừng bỏ qua bài chia sẻ dưới đây nhé!

• Vai trò của kiến trúc bảo mật thích ứng trong quản lý ninh mạng
• Ưu điểm khi kết hợp trí tuệ nhân tạo AI và RPA - Robotic Process Automation
• Trung tâm xSeries FUNiX ra mắt môn Cơ sở dữ liệu và giải thuật
• Cấu trúc dữ liệu là gì? Những điều cần biết về cấu trúc dữ liệu
• Làm thế nào để học lập trình? Mẹo hay cho người mới bắt đầu

>> Khóa học lập trình cơ bản 

>> Kỹ thuật lập trình PHP 

1. Hướng dẫn giải một số bài toán tìm đường đi ngắn nhất trong cấu trúc dữ liệu và giải thuật

Bài toán tìm đường đi ngắn nhất trong cấu trúc dữ liệu và giải thuật: 

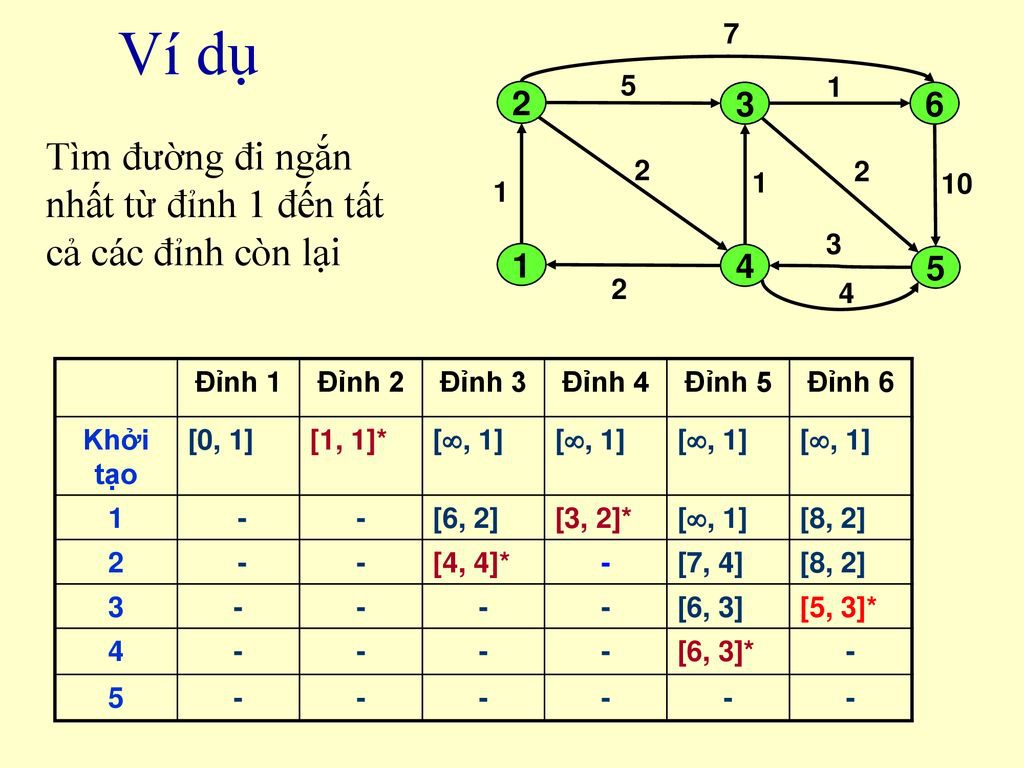
Cho đồ thị có trọng số G = (A, E), hãy tìm một đường đi ngắn nhất từ đỉnh xuất phát S ∈ A đến đỉnh đích F ∈ A. Độ dài của đường đi này được ký hiệu là d[S, F] hay còn gọi là khoảng cách từ S đến F. Nếu như không tồn tại đường đi từ S tới F thì ta sẽ đặt khoảng cách đó = +∞.

Trường hợp, đồ thị có chu trình âm thì khoảng cách giữa một số cặp đỉnh nào đó có thể không xác định.

Trường hợp, đồ thị không có chu trình âm thì có thể chứng minh một trong những đường đi ngắn nhất là đường đi cơ bản. Và nếu như biết được khoảng cách từ S tới tất cả những đỉnh khác thì đường đi ngắn nhất từ S tới F có thể tìm được bởi thuật toán sau:

• Gọi c[u, v] là trọng số của cạnh [u, v]. 
• Quy ước c[v, v] = 0 với mọi v ∈ VA và c[u, v] = +∞ nếu như (u, v) ∉ E. 
• Đặt d[S, v] là khoảng cách từ S tới v. 
• Để tìm đường đi từ S tới F,  thì luôn tồn tại đỉnh F1 ≠ F sao cho: d[S, F] = d[S, F1] + c[F1, F]
• Nghĩa là: Độ dài đường đi ngắn nhất S đến F = Độ dài đường đi ngắn nhất S đến F1 + Chi phí đi từ F1 tới F.
• Đỉnh F1 đó là đỉnh liền trước F trong đường đi ngắn nhất từ S tới F. 
• Nếu F1≡S thì đường đi ngắn nhất là đường đi trực tiếp theo cung (S, F). 
• Nếu không thì vấn đề trở thành tìm đường đi ngắn nhất từ S tới F1. Và ta lại tìm được một đỉnh F2 khác F và F1 để: d[S, F1] = d[S, F2] + c[F2, F1].
• Cứ như vậy, sau một số bước ta thu được dãy F, F1, F2, … không chứa đỉnh lặp lại và kết thúc ở S. Lật ngược thứ tự dãy ta sẽ có được kết quả đường đi ngắn nhất từ S tới F.

Tuy nhiên, thường thì người ta sẽ không sử dụng phương pháp này mà sẽ kết hợp lưu vết đường đi ngay trong quá trình tìm kiếm.

Hãy cùng xét một số thuật toán tìm đường đi ngắn nhất từ đỉnh S tới đỉnh F trên đơn đồ thị có hướng G = (A, E) có n đỉnh và m cung. Trong trường hợp đơn đồ thị vô hướng với trọng số không âm, bài toán tìm đường đi ngắn nhất có thể dẫn về bài toán trên đồ thị có hướng bằng cách thay mỗi cạnh của nó bằng hai cung có hướng ngược chiều nhau. 

Input: file văn bản MINPATH.INP

Trong đó: 

• Dòng 1: Chứa số đỉnh n ( ≤ 100), số cung m của đồ thị, đỉnh xuất phát S, đỉnh đích F cách nhau ít nhất 1 dấu cách.
• m dòng tiếp theo, mỗi dòng có dạng ba số u, v, c[u, v] cách nhau ít nhất 1 dấu cách, thể hiện (u, v) là một cung ∈ E và trọng số của cung đó là c[u,v] (c[u, v] là số nguyên có giá trị tuyệt đối ≤ 100).

Output: file văn bản MINPATH.OUT ghi đường đi ngắn nhất từ S tới F và độ dài đường đi đó.

>>> ĐỌC NGAY: Mức lương của Kỹ sư dữ liệu trong năm 2023 như thế nào

2. Hướng dẫn giải bài toán tô màu trên đồ thị trong cấu trúc dữ liệu và giải thuật

Bài toán tô màu đồ thị trong cấu trúc dữ liệu và giải thuật được sử dụng nhiều. Theo đó, đây là việc thực hiện gán màu cho mỗi đỉnh của đồ thị, sao cho hai đỉnh kề nhau không cùng một màu và số màu được sử dụng là ít nhất. 

Trong đó: số màu ít nhất có thể sử dụng để tô màu đồ thị được gọi là sắc số của đồ thị đó.

Thuật toán tô màu đồ thị có thể được trình bày một cách dễ hiểu qua các bước thuật toán sau đây:

• Input:  đồ thị G = (V, E).
• Output: đồ thị G = (V, E) có các đỉnh đã được gán màu.

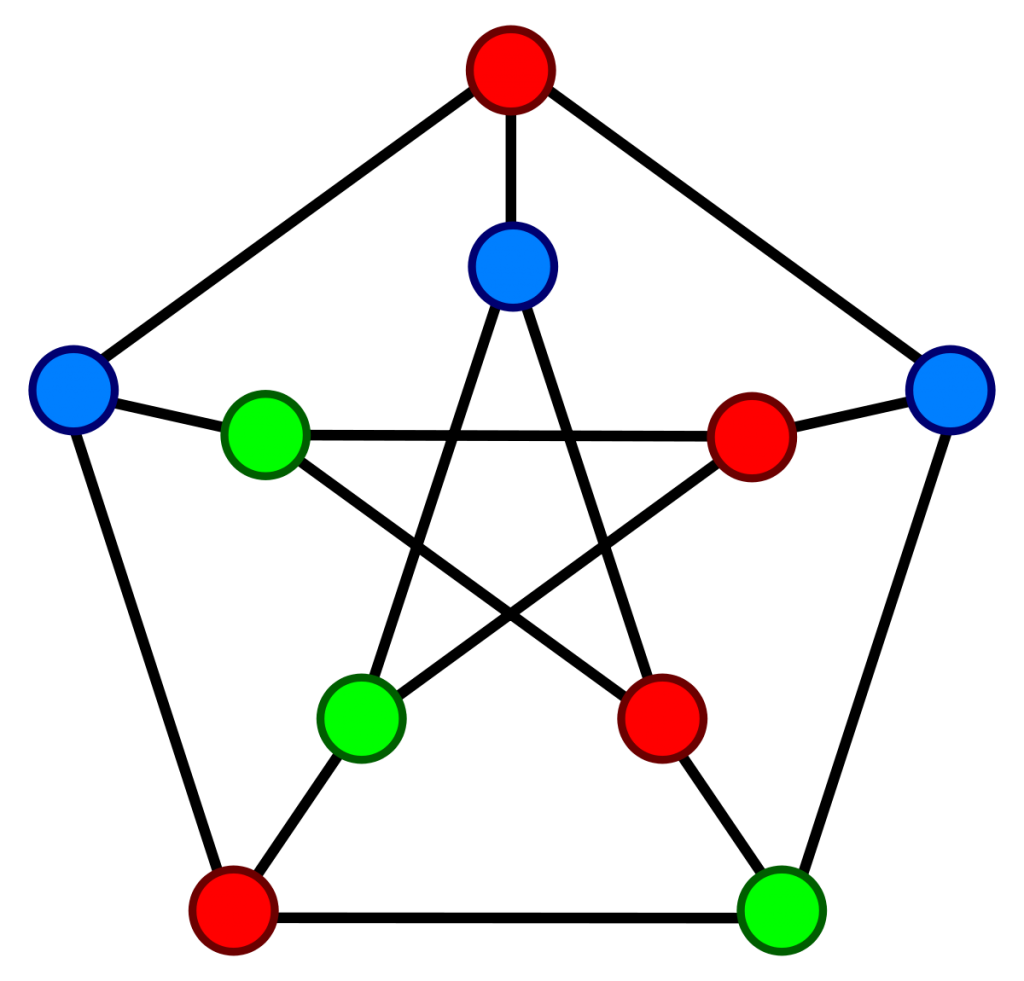
Các bước thực hiện của thuật toán:

Bước 1: Tính giá trị bậc của các đỉnh trong V. Lập danh sách V’:=[v1tv2, …,vn] là các đỉnh của đồ thị được sắp xếp theo thứ tự bậc giảm dần: d(v1) > d(v2) > … > d(vn). Lúc đầu, tất cả các đỉnh trong V (V’) chưa được tô màu. Gán i := 1;

Bước 2: Tô màu i cho đỉnh đầu tiên trong danh sách V’. Duyệt lần lượt các đỉnh khác trong V’(nếu có) và chỉ tô màu i cho các đỉnh không kể những đỉnh đã có màu i.

Bước 3: Kiểm tra nếu tất cả các đỉnh trong V đã được tô màu thì thuật toán kết thúc, đồ thị đã sử dụng  i màu để tô. Ngược lại, nếu vẫn còn đỉnh chưa được tô thì chuyển sang bước tiếp theo.

Bước 4: Loại khỏi danh sách V’ các đỉnh đã tô màu. Sắp xếp lại các đỉnh trong V’ theo thứ tự bậc giảm dần. Gán i := i + 1 và quay lại bước 2.

>>> ĐỌC THÊM: Kỹ sư dữ liệu làm gì? Tại sao nên theo đuổi sự nghiệp kỹ sư dữ liệu

Mong rằng qua bài viết hướng dẫn giải 1 số bài toán tìm đường đi ngắn nhất và tô màu trên đồ thị trong cấu trúc dữ liệu và giải thuật của FUNiX trên đây, có thể giúp bạn giải quyết nhiều bài toán quan trọng được đặt ra trong thực tiễn.

>>> Nếu bạn đang có nhu cầu học lập trình trực tuyến, tìm hiểu ngay tại đây:

>>> Xem thêm các chủ đề hữu ích:

Phân tích dữ liệu kinh doanh là làm gì năm 2022

Data analyst là gì? Tất cả những gì cần biết về nghề phân tích dữ liệu Data analyst

Nhà phân tích dữ liệu so với Nhà khoa học dữ liệu: Sự khác biệt là gì?

Trang bị Kỹ năng phân tích dữ liệu cho người mới

Nhà phân tích dữ liệu làm gì: mô tả, trách nhiệm?

Giải đáp về Các loại nhà phân tích dữ liệu Data Analyst

Phạm Thị Thanh Ngọc