Merge sort là một thuật toán sắp xếp dựa trên kỹ thuật “chia để trị”. Đây là một trong những thuật toán sắp xếp hiệu quả nhất.

Trong bài viết này, bạn sẽ tìm hiểu về hoạt động của thuật toán merge sort, độ phức tạp về thời gian và không gian của nó cũng như việc triển khai nó trong các ngôn ngữ lập trình khác nhau như C ++, Python và JavaScript.

1. Thuật toán merge sort hoạt động như thế nào?

Merge sort hoạt động trên nguyên tắc chia để trị. Merge sort chia nhỏ nhiều lần một mảng (array) thành hai mảng con bằng nhau cho đến khi mỗi mảng con (subarray) bao gồm một phần tử duy nhất. Cuối cùng, tất cả các mảng con đó được hợp nhất để sắp xếp mảng kết quả.

Khái niệm này có thể được giải thích hiệu quả hơn với sự trợ giúp của một ví dụ. Hãy xem xét một mảng không được sắp xếp với các phần tử sau: {16, 12, 15, 13, 19, 17, 11, 18}.

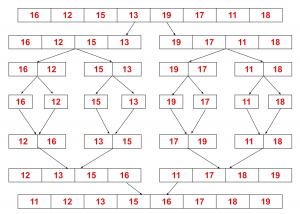
Ở đây, thuật toán merge sort chia mảng thành hai nửa, calls itself for the two halves (tự gọi mảng cho hai nửa) và sau đó hợp nhất hai nửa đã sắp xếp.

>>> Xem thêm: Giới thiệu về thuật toán sắp xếp Shell sort

2. Thuật toán merge sort

Dưới đây là thuật toán của merge sort:

MergeSort(arr[], leftIndex, rightIndex)
if leftIndex >= rightIndex
     return
else
     Find the middle index that divides the array into two halves:  
             middleIndex = leftIndex + (rightIndex-leftIndex)/2
     Call mergeSort() for the first half:   
             Call mergeSort(arr, leftIndex, middleIndex)
     Call mergeSort() for the second half:
             Call mergeSort(arr, middleIndex+1, rightIndex)
     Merge the two halves sorted in step 2 and 3:
             Call merge(arr, leftIndex, middleIndex, rightIndex)

3. Độ phức tạp về thời gian và bộ nhớ của thuật toán merge sort

Thuật toán merge sort có thể được biểu diễn dưới dạng quan hệ lặp lại sau:

T (n) = 2T (n / 2) + O (n)

Sau khi giải quan hệ lặp lại này bằng cách sử dụng định lý thợ (master’s theorem) hoặc phương pháp cây đệ quy (recurrence tree), bạn sẽ nhận được nghiệm (solution) là O (n logn). Do đó, độ phức tạp về thời gian (time complexity) của thuật toán merge sort là O (n logn) .

Độ phức tạp thời gian trong trường hợp tốt nhất của merge sort: O (n logn)

Độ phức tạp thời gian theo trường hợp trung bình của merge sort: O (n logn)

Độ phức tạp thời gian trong trường hợp xấu nhất của merge sort: O (n logn)

Độ phức tạp của bộ nhớ phụ (auxiliary space complexity) của thuật toán merge sort là O (n) vì n bộ nhớ phụ được yêu cầu trong việc thực hiện merge sort. 

>>> Xem thêm: Các khóa học lập trình C++ online phù hợp với người mới

4. Triển khai thuật toán merge sort 

Dưới đây là cách triển khai thuật toán merge sort trong C ++:

// C++ implementation of the
// merge sort algorithm
#include <iostream>
using namespace std;
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
void merge(int arr[], int leftIndex, int middleIndex, int rightIndex)
{
 int leftSubarraySize = middleIndex - leftIndex + 1;
 int rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
 int L[leftSubarraySize], R[rightSubarraySize];
// Copying data to temporary arrays L[] and R[]
 for (int i = 0; i < leftSubarraySize; i++)
 L[i] = arr[leftIndex + i];
 for (int j = 0; j < rightSubarraySize; j++)
 R[j] = arr[middleIndex + 1 + j];
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
 int i = 0;
// Initial index of Right subarray
 int j = 0;
// Initial index of merged subarray
 int k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
 {
 if (L[i] <= R[j])
 {
 arr[k] = L[i];
 i++;
 }
 else
 {
 arr[k] = R[j];
 j++;
 }
 k++;
 }
// If there're some remaining elements in L[]
// Copy to arr[]
 while (i < leftSubarraySize)
 {
 arr[k] = L[i];
 i++;
 k++;
 }
// If there're some remaining elements in R[]
// Copy to arr[]
 while (j < rightSubarraySize)
 {
 arr[k] = R[j];
 j++;
 k++;
 }
}
void mergeSort(int arr[], int leftIndex, int rightIndex)
{
 if(leftIndex >= rightIndex)
 {
 return;
 }
 int middleIndex = leftIndex + (rightIndex - leftIndex)/2;
 mergeSort(arr, leftIndex, middleIndex);
 mergeSort(arr, middleIndex+1, rightIndex);
 merge(arr, leftIndex, middleIndex, rightIndex);
}

// Function to print the elements
// of the array
void printArray(int arr[], int size)
{
 for (int i = 0; i < size; i++)
 {
 cout << arr[i] << " ";
 }
 cout << endl;
}
// Driver code
int main()
{
 int arr[] = { 16, 12, 15, 13, 19, 17, 11, 18 };
 int size = sizeof(arr) / sizeof(arr[0]);
cout << "Unsorted array:" << endl;
 printArray(arr, size);
mergeSort(arr, 0, size - 1);
cout << "Sorted array:" << endl;
 printArray(arr, size);
return 0;
}

Đầu ra:

Unsorted array:
16 12 15 13 19 17 11 18 
Sorted array:
11 12 13 15 16 17 18 19

5. Triển khai Thuật toán merge sort trong JavaScript 

Dưới đây là cách triển khai Thuật toán merge sort trong JavaScript

// JavaScript implementation of the
// merge sort algorithm
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
function merge(arr, leftIndex, middleIndex, rightIndex) {
 let leftSubarraySize = middleIndex - leftIndex + 1;
 let rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
 var L = new Array(leftSubarraySize);
 var R = new Array(rightSubarraySize);
// Copying data to temporary arrays L[] and R[]
 for(let i = 0; i<leftSubarraySize; i++) {
 L[i] = arr[leftIndex + i];
 }
 for (let j = 0; j<rightSubarraySize; j++) {
 R[j] = arr[middleIndex + 1 + j];
 }
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
 var i = 0;
// Initial index of Right subarray
 var j = 0;
// Initial index of merged subarray
 var k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
 {
 if (L[i] <= R[j])
 {
 arr[k] = L[i];
 i++;
 }
 else
 {
 arr[k] = R[j];
 j++;
 }
 k++;
 }
// If there're some remaining elements in L[]
// Copy to arr[]
 while (i < leftSubarraySize)
 {
 arr[k] = L[i];
 i++;
 k++;
 }
// If there're some remaining elements in R[]
// Copy to arr[]
 while (j < rightSubarraySize)
 {
 arr[k] = R[j];
 j++;
 k++;
 }
}
function mergeSort(arr, leftIndex, rightIndex) {
 if(leftIndex >= rightIndex) {
 return
 }
 var middleIndex = leftIndex + parseInt((rightIndex - leftIndex)/2);
 mergeSort(arr, leftIndex, middleIndex);
 mergeSort(arr, middleIndex+1, rightIndex);
 merge(arr, leftIndex, middleIndex, rightIndex);
}
// Function to print the elements
// of the array
function printArray(arr, size) {
 for(let i = 0; i<size; i++) {
 document.write(arr[i] + " ");
 }
 document.write("<br>");
}
// Driver code:
var arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ];
var size = arr.length;
document.write("Unsorted array:<br>");
printArray(arr, size);
mergeSort(arr, 0, size - 1);
document.write("Sorted array:<br>");
printArray(arr, size);

Đầu ra:

Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19

6. Triển khai thuật toán merge sort trong Python

Dưới đây là triển khai của thuật toán merge sort trong Python:

# Python implementation of the
# merge sort algorithm
def mergeSort(arr):
    if len(arr) > 1:
        # Finding the middle index of the array
        middleIndex = len(arr)//2
        # Left half of the array
        L = arr[:middleIndex]
        # Right half of the array
        R = arr[middleIndex:]
        # Sorting the first half of the array
        mergeSort(L)
        # Sorting the second half of the array
        mergeSort(R)
        # Initial index of Left subarray
        i = 0
        # Initial index of Right subarray
        j = 0
        # Initial index of merged subarray
        k = 0
        # Copy data to temp arrays L[] and R[]
        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i = i + 1
            else:
                arr[k] = R[j]
                j = j + 1
            k = k + 1
        # Checking if there're some remaining elements
        while i < len(L):
            arr[k] = L[i]
            i = i + 1
            k = k + 1
        while j < len(R):
            arr[k] = R[j]
            j = j + 1
            k = k + 1
# Function to print the elements
# of the array
def printArray(arr, size):
    for i in range(size):
        print(arr[i], end=" ")
    print()

# Driver code
arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ]
size = len(arr)
print("Unsorted array:")
printArray(arr, size)
mergeSort(arr)
print("Sorted array:")
printArray(arr, size)

Đầu ra:

Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19

7. Hiểu các thuật toán sắp xếp khác

Sắp xếp (sorting) là một trong những thuật toán được sử dụng nhiều nhất trong lập trình. Bạn có thể sắp xếp các phần tử trong các ngôn ngữ lập trình khác nhau bằng cách sử dụng các thuật toán sắp xếp khác nhau như quick sort, bubble sort, merge sort, insertion sort, etc. 

>>> Nếu bạn đang có nhu cầu tìm hiểu về khóa học lập trình đi làm ngay. Hãy liên hệ với FUNiX ngay tại đây:

>>> Xem thêm chuỗi bài viết liên quan:

Các bước tự học lập trình c++ hiệu quảyến FUNiX

FUNiX – Học lấy bằng đại học trực tuyến giá trị ngang bằng đại học chính quy

Lập trình khoa học máy tính – Ngành nghề Hot cho các bạn trẻ

Học lập trình Python có phù hợp với người trái ngành

Nên học ngôn ngữ lập trình Ruby hay học ngôn ngữ lập trình Python?

Vân Nguyễn

Dịch từ: https://www.makeuseof.com/merge-sort-algorithm/