Binary Search Tree (Cây tìm kiếm nhị phân) rất có ích trong việc tổ chức dữ liệu. Bài viết này sẽ giải thích đầy đủ về cách chúng hoạt động.

• Vai trò của kiến trúc bảo mật thích ứng trong quản lý ninh mạng
• Ưu điểm khi kết hợp trí tuệ nhân tạo AI và RPA - Robotic Process Automation
• Cấu trúc dữ liệu là gì? Những điều cần biết về cấu trúc dữ liệu
• Làm thế nào để học lập trình? Mẹo hay cho người mới bắt đầu
• Trung tâm Công nghệ chuyên sâu xSeries ra mắt phiên bản mới môn Toán rời rạc

Binary Search Tree là một trong những cấu trúc dữ liệu khác nhau giúp tổ chức và sắp xếp dữ liệu. Nó rất linh hoạt và là một cách hiệu quả để lưu trữ dữ liệu theo hệ thống phân cấp.

Trong bài viết này, chúng ta sẽ xem xét kỹ hơn cách thức hoạt động — cũng như các thuộc tính và ứng dụng của Binary Search Tree.

1. Binary Search Tree là gì?

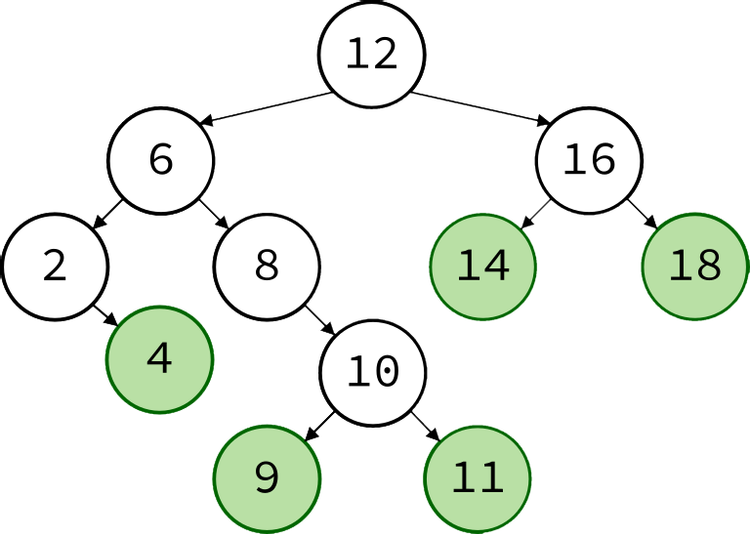
Binary Search Tree là một cấu trúc dữ liệu bao gồm các nút (node) — tương tự như Linked Lists (Danh sách được liên kết). Có hai loại nút: parent (nút cha) và child (nút con). Root node (nút gốc) là điểm đầu của cấu trúc phân nhánh thành hai nút con, được gọi là left node (nút bên trái) và right node (nút bên phải).

Mỗi nút chỉ có thể được tham chiếu bởi parent của nó và chúng ta có thể đi qua các nút của cây tùy thuộc vào hướng. Binary Search Tree có ba thuộc tính chính:

1. Nút bên trái nhỏ hơn nút cha của nó.
2. Nút bên phải lớn hơn nút cha của nó.
3. Các cây con bên trái và bên phải bắt buộc phải là Binary Search Tree.

Chúng ta đạt được Binary Search Tree hoàn hảo khi tất cả các cấp được lấp đầy và mọi nút đều có nút con bên trái và bên phải.

>>> Xem thêm: Hướng dẫn sử dụng cấu trúc cây, cây tìm kiếm nhị phân

2. Các hoạt động cơ bản của cây tìm kiếm nhị phân

Bây giờ bạn đã hiểu rõ hơn về định nghĩa Binary Search Tree, hãy cùng xem xét các operation (hoạt động) cơ bản của nó.

2.1 Search (Tìm kiếm)

Tìm kiếm cho phép xác định một giá trị cụ thể có trong cây. Chúng ta có thể sử dụng hai loại tìm kiếm: tìm kiếm theo chiều rộng (breadth-first search, hay BFS) và tìm kiếm theo chiều sâu (depth-first search, hay DFS). Tìm kiếm theo chiều rộng là một thuật toán tìm kiếm bắt đầu từ nút gốc và di chuyển theo chiều ngang, từ bên này sang bên kia, cho đến khi tìm thấy mục tiêu. Mỗi nút được truy cập một lần trong quá trình tìm kiếm này.

Mặt khác, tìm kiếm theo chiều sâu đi qua cây theo chiều dọc – bắt đầu từ nút gốc và đi dọc xuống một nhánh duy nhất. Nếu mục tiêu được tìm thấy, operation kết thúc. Nhưng nếu không, nó sẽ tìm kiếm các nút khác.

2.2 Insert (Chèn)

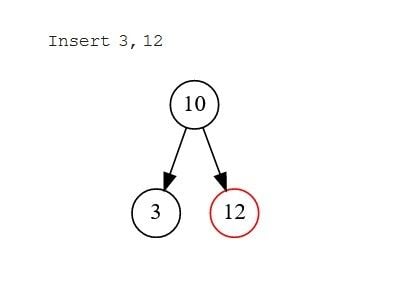
Thao tác chèn sử dụng thao tác tìm kiếm để xác định vị trí nơi nút mới sẽ được chèn. Quá trình này bắt đầu từ nút gốc và quá trình tìm kiếm bắt đầu cho đến khi đến đích. Có ba trường hợp cần xem xét:.

• Trường hợp 1: Khi không có nút nào tồn tại. Nút được chèn vào sẽ trở thành nút gốc.

• Trường hợp 2: Không có con. Trong trường hợp này, nút được chèn sẽ được so sánh với nút gốc. Nếu nó lớn hơn, nó sẽ trở thành nút con bên phải; nếu không, nó sẽ trở thành nút con trái.

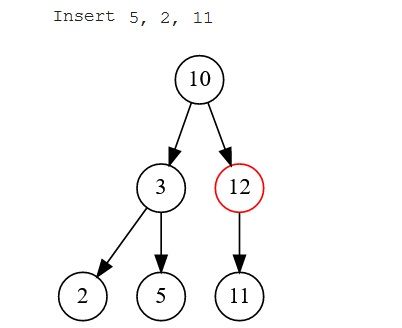
• Trường hợp 3: Khi có cả nút gốc và con của nó. Nút mới sẽ được so sánh với mỗi nút trên đường dẫn của nó để xác định nút nào nó sẽ truy cập tiếp theo. Nếu nút này lớn hơn nút gốc, nó sẽ đi qua cây con bên phải, nếu không thì bên trái. Tương tự, so sánh được thực hiện ở mỗi cấp độ để xác định xem nó sẽ đi sang phải hay sang trái cho đến khi đến đích.

2.3 Delete (Xóa)

Thao tác xóa được sử dụng để xóa một nút cụ thể trong cây. Việc này khá phức tạp vì sau khi xóa một nút, cây phải được tổ chức lại cho phù hợp. Có ba trường hợp chính cần xem xét:

• Trường hợp 1: Xóa một nút lá (leaf node). Nút lá là nút không có nút con nào. Đây là nút dễ nhất để loại bỏ vì nó không ảnh hưởng đến bất kỳ nút nào khác; chúng ta chỉ cần đi dọc cây cho đến khi đến vị trí của nó và xóa nó đi.

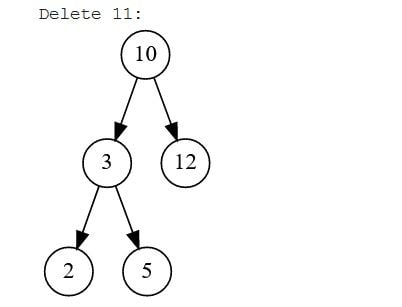
• Trường hợp 2: Xóa một nút cha có một nút con. Việc này sẽ dẫn đến việc nút con chiếm vị trí của nó và tất cả các nút tiếp theo sẽ tăng lên một cấp. Sẽ không có thay đổi về cấu trúc cây con.

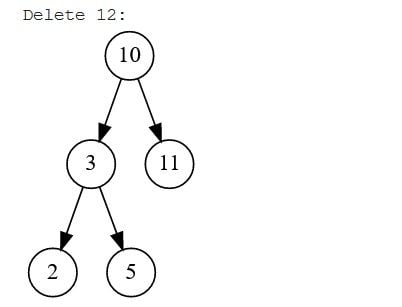
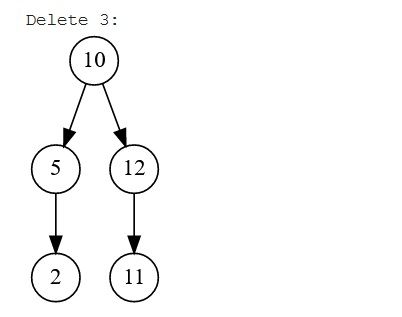
• Trường hợp 3: Xóa một nút cha có hai nút con. Khi loại bỏ một nút có hai nút con, trước tiên chúng ta phải tìm một nút tiếp theo có thể thay thế vị trí của nó. Hai nút có thể thay thế nút đã bị loại bỏ: inorder successor hoặc inorder predecessor. Inorder successor là con ngoài cùng bên trái của cây con bên phải và inorder predecessor là con ngoài cùng bên phải của cây con bên trái. Chúng ta sẽ sao chép nội dung của nút successor (kế nhiệm)/predecessor (tiền nhiệm) và xóa inorder successor/predecessor.

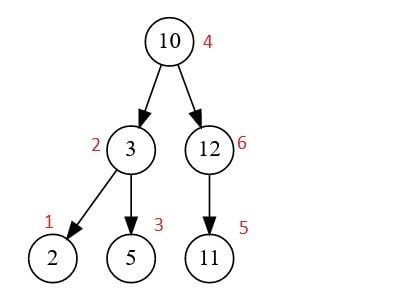
3. Làm thế nào để duyệt (traverse) một Binary Search Tree

Traversal là quá trình mà qua đó chúng ta điều hướng Binary Search Tree. Nó được thực hiện để xác định vị trí một mục cụ thể hoặc để in outline (khung) của cây. Chúng ta luôn bắt đầu từ nút gốc và phải đi theo các cạnh để đến các nút khác. Mỗi nút nên được coi là một cây con và quá trình này được lặp lại cho đến khi tất cả các nút được truy cập.

• In-order traversal: sẽ tạo ra một bản đồ theo thứ tự tăng dần. Với phương pháp này, chúng ta bắt đầu từ cây con bên trái và tiếp tục đến cây con gốc và cây con bên phải.

• Post-order traversal: Trong phương pháp này, nút gốc được truy cập đầu tiên, tiếp theo là cây con bên trái và cây con bên phải.

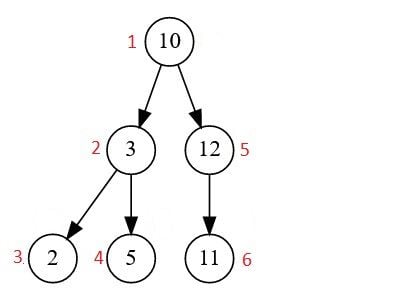
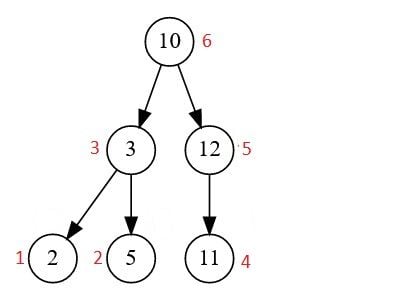
• Post-Order Traversal: truy cập vào nút gốc cuối cùng. Chúng ta bắt đầu từ cây con bên trái, sau đó đến cây con bên phải, và sau đó là nút gốc.

>>> Xem thêm: Làm thế nào để trở thành một kiến ​​trúc sư dữ liệu?

4. Ứng dụng trong thế giới thực

Làm thế nào để chúng ta sử dụng các thuật toán cây tìm kiếm nhị phân? Như bạn có thể đoán được, chúng cực kỳ hiệu quả trong việc tìm kiếm và phân loại. Sức mạnh lớn nhất của cây nhị phân là cấu trúc có tổ chức của nó. Nó cho phép thực hiện tìm kiếm với tốc độ đáng kể bằng cách cắt giảm một nửa lượng dữ liệu chúng ta cần phân tích.

Binary Search Tree cho phép chúng ta duy trì một cách hiệu quả tập dữ liệu thay đổi động ở dạng có tổ chức. Đối với các ứng dụng có dữ liệu được chèn và gỡ bỏ thường xuyên, chúng rất hữu ích. Công cụ trò chơi điện tử sử dụng một thuật toán dựa trên cây được gọi là phân vùng không gian nhị phân để giúp hiển thị các đối tượng một cách có trật tự. Microsoft Excel và hầu hết các phần mềm bảng tính sử dụng cây nhị phân làm cấu trúc dữ liệu cơ bản của chúng.

Bạn có thể ngạc nhiên khi biết rằng mã Morse sử dụng cây tìm kiếm nhị phân để mã hóa dữ liệu. Một lý do khác khiến Binary Search Tree rất hữu ích là do chúng có nhiều biến thể. Tính linh hoạt của chúng đã dẫn đến nhiều biến thể được tạo ra để giải quyết tất cả các loại vấn đề. 

5. Binary Search Tree: Điểm khởi đầu hoàn hảo

Một trong những cách chính để đánh giá chuyên môn của một kỹ sư là thông qua kiến ​​thức và ứng dụng của họ về cấu trúc dữ liệu. Cấu trúc dữ liệu rất hữu ích và có thể giúp tạo ra một hệ thống hiệu quả hơn. Binary Search Tree là một khởi điểm tuyệt vời cho bất kỳ nhà phát triển nào để làm quen với cấu trúc dữ liệu.

Dịch từ: https://www.makeuseof.com/what-is-a-binary-search-tree/

>>> Nếu bạn đang có nhu cầu tìm hiểu về khóa học lập trình đi làm ngay. Hãy liên hệ với FUNiX ngay tại đây:

>>> Xem thêm chuỗi bài viết liên quan:

Ứng dụng học máy trong phân tích dữ liệu

5 công cụ phần mềm phân tích dữ liệu

Phân tích dữ liệu kinh doanh là làm gì năm 2022

Data analyst là gì? Tất cả những gì cần biết về nghề phân tích dữ liệu Data analyst

Vân Nguyễn