Hướng dẫn sử dụng cấu trúc cây, cây tìm kiếm nhị phân
Có nhiều ứng dụng trong việc giải các bài toán máy tính. Bởi lẽ việc biểu diễn và triển khai cây trong bộ nhớ trong rất đơn giản. Trong bài viết dưới đây, hãy cùng FUNiX tìm hiểu một số kiến thức liên quan đến cây nhị phân và cách sử dụng cấu trúc cây nhé!
>> Các kiểu dữ liệu trong Javascript
Tìm hiểu các khái niệm liên quan đến cấu trúc cây
Cấu trúc dữ liệu trừu tượng mà chúng ta quan tâm trong bài viết này là cấu trúc cây. Cây là một cấu trúc dữ liệu bao gồm một tập hợp hữu hạn các nút, và tồn tại một mối quan hệ phân cấp gọi là mối quan hệ “cha-con” giữa các nút, trong đó có một nút đặc biệt được gọi là gốc.
Một cây có thể được định nghĩa một cách đệ quy như sau:
- Mỗi nút là một cây và nút đó cũng là gốc của cây đó.
- Nếu n là một nút thì n1, n2, …, nk lần lượt là gốc của các cây T1, T2, …, Tk; các cây này không có nút chung. Khi đó nếu nút n trở thành nút cha của các nút n1, n2, …, nk, chúng ta sẽ nhận được một cây T mới. Cây này có gốc tại nút n, và các cây T1, T2, …, Tk trở thành cây con.
Hãy xem xét cây trong hình dưới đây để hiểu sơ qua về cách sử dụng cấu trúc cây:
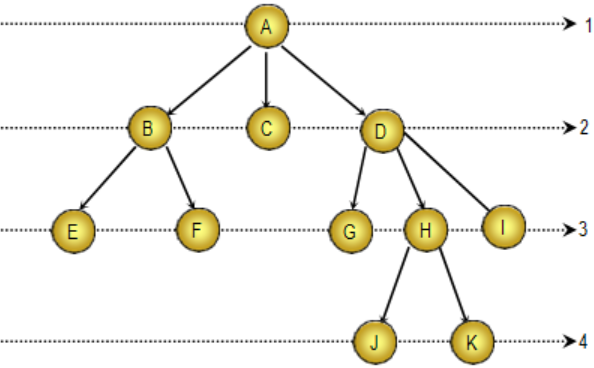

- A là cha của B, C và D, và G, H, và I là con của D.
- Số nút con của một nút được gọi là hạng của nút, ví dụ, A có hạng 3, B có hạng 2 và C có hạng 0.
- Các nút ở mức 0 được gọi là nút lá hoặc nút đầu cuối. Ví dụ ở trên, các nút E, F, C, G, J, K và I là các nút lá. Các nút không phải là lá được gọi là nút nhánh.
- Gốc của cây được gán mức 1, và nếu nút cha ở mức i thì nút con ở mức i + 1.
- Chiều cao hoặc chiều sâu của cây là số lượng nút tối đa trong cây đó. Cây trên có chiều cao là 4.
Ví dụ:
- Mục lục của sách, bao gồm các chương, chương, bài, … có cấu trúc dạng cây.
- Cấu trúc thư mục trên đĩa cũng có cấu trúc cây, và thư mục gốc có thể coi là thư mục gốc của cây.
- Các cây con là các thư mục con và tệp trên thư mục gốc.
- Gia phả của một dòng tộc cũng có cấu trúc giống cây.
- Các biểu thức số học bao gồm các phép toán cộng, trừ, nhân và chia cũng có thể được lưu trữ trong một cây, trong đó các toán hạng được lưu trữ trong các nút lá và các toán tử được lưu trữ trong các nút nhánh, mỗi nhánh là một biểu thức con.
Cây nhị phân (binary tree)
Cây nhị phân là một dạng cấu trúc cây quan trọng. Nó được đặc trưng bởi thực tế là mỗi nút trong cây có nhiều nhất hai nhánh con. Đối với một nút, cũng có thể phân biệt các cây con bên trái và bên phải của nút.
Các tính chất của cây nhị phân như sau:
- Trong số các cây nhị phân có cùng số nút, chiều cao của cây nhị phân suy biến là cao nhất và chiều cao của cây nhị phân hoàn chỉnh là nhỏ nhất.
- Số nút tối đa ở mức i của cây nhị phân là 2i-1 và số nút tối thiểu là 1 (i ≥ 1).
- Số nút tối đa trên cây nhị phân có độ cao h là 2h-1 và số nút tối thiểu là h (h ≥ 1). Chiều cao h = [log2 (n + 1)] + 1 đối với cây nhị phân hoàn toàn không đầy đủ với n nút.
- Chiều cao của một cây nhị phân hoàn chỉnh với n nút là h = log2 (n + 1).
2 cách biểu diễn cây nhị phân
Biểu diễn mảng
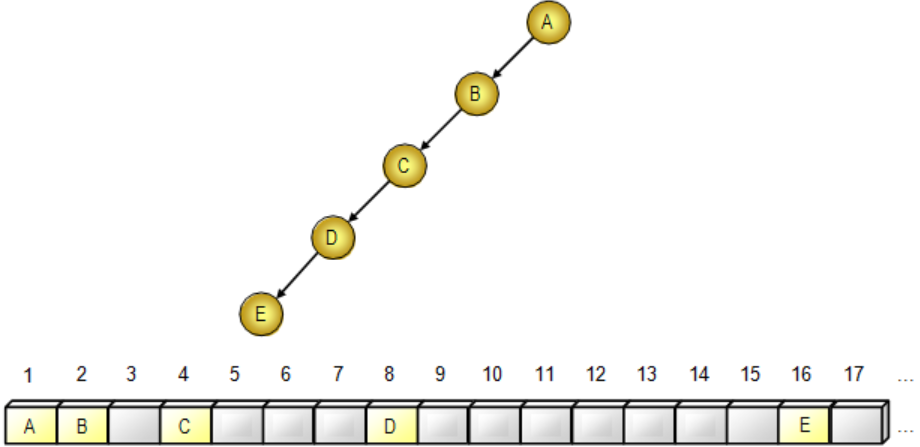
Nếu chúng ta có một cây nhị phân hoàn chỉnh, chúng ta có thể dễ dàng đánh số các nút trong cây, bắt đầu từ cấp 1 và làm việc theo từng cấp, với các nút ở mỗi cấp được đánh số từ trái sang phải.
Sử dụng số này, các nút con của nút thứ i sẽ là các nút thứ 2i và 2i + 1. Cha của nút thứ j là nút div 2 thứ j. Từ đó cây có thể được lưu trữ trong mảng T, nút thứ i của cây được lưu trữ là phần tử T [i].
Ví dụ, đối với một cây nghiêng trái, chúng ta phải sử dụng một mảng 31 phần tử để lưu trữ một cây nhị phân chỉ có 5 nút.

Biểu diễn bằng cấu trúc liên kết
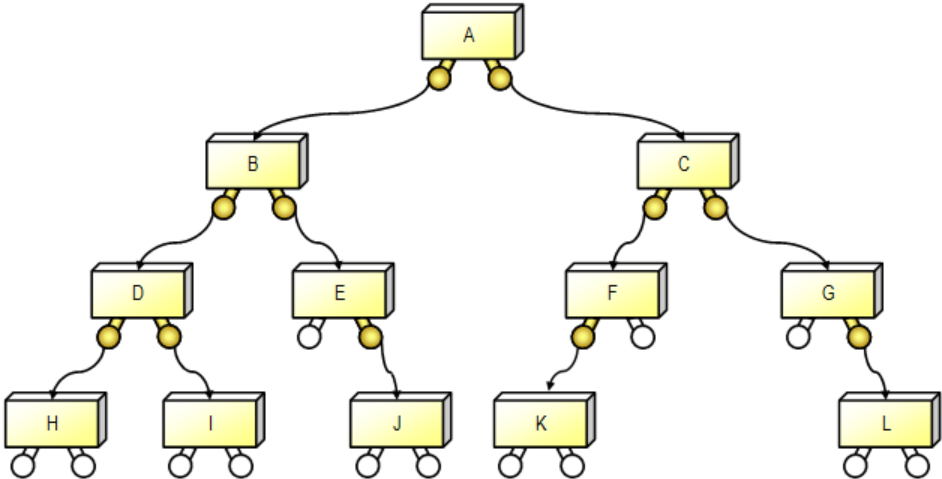
Khi một cây nhị phân được biểu diễn theo cấu trúc liên kết, mỗi nút của cây là một bản ghi bao gồm 3 trường:
- Trường thông tin: Chứa giá trị được lưu trữ tại nút này.
- Trường bên trái: chứa liên kết (con trỏ) đến nút con bên trái, tức là chứa đủ thông tin để biết nút con bên trái của nút nào, nếu không có con bên trái thì gán giá trị đặc biệt cho trường.
- Trường bên phải: chứa liên kết (con trỏ) tới nút con bên phải, tức là chứa đủ thông tin để biết nút con bên phải của nút nào, nếu không có con bên phải thì trường này được gán một giá trị đặc biệt.
Đối với một cây, chúng ta chỉ cần quan tâm đến việc giữ nút gốc, bởi vì bắt đầu từ nút gốc, theo hướng của các liên kết trái và phải, tất cả các nút khác có thể được duyệt.

3 cách duyệt cây nhị phân
Để biết cách sử dụng cấu trúc cây, bạn cần nắm chắc 3 phép duyệt cây nhị phân sau:
Preorder traversal (duyệt theo thứ tự trước)
Trong phép duyệt này, giá trị trong bất kỳ nút nào sẽ được liệt kê trước các giá trị được lưu trữ trong hai nút con của nó, có thể được mô tả bằng quy trình đệ quy sau:
|
procedure Visit(N); {Duyệt nhánh cây nhận N là nút gốc của nhánh đó} begin if N ≠ nil then begin <Output trường Info của nút N> Visit(Nút con trái của N); Visit(Nút con phải của N); end; end; |
Các giá trị được liệt kê theo thứ tự: A B D H I E J C F K G L.
Inorder traversal (duyệt theo thứ tự giữa)
Giá trị trong bất kỳ nút nào sẽ được liệt kê sau giá trị được lưu trữ trong nút con bên trái và trước giá trị được lưu trữ trong nút con bên phải của nút đó, có thể được mô tả bằng quy trình đệ quy sau:
|
procedure Visit(N); {Duyệt nhánh cây nhận N là nút gốc của nhánh đó} begin if N ≠ nil then begin Visit(Nút con trái của N); <Output trường Info của nút N> Visit(Nút con phải của N); end; end; |
Các giá trị được liệt kê theo thứ tự: H D I B E J A K F C G L.
Postorder traversal (duyệt theo thứ tự sau)
Giá trị trong bất kỳ nút nào được liệt kê sau giá trị được lưu trữ trong hai nút con của nút, có thể được mô tả bằng quy trình đệ quy sau:
|
procedure Visit(N); {Duyệt nhánh cây nhận N là nút gốc của nhánh đó} begin if N ≠ nil then begin Visit(Nút con trái của N); Visit(Nút con phải của N); <Output trường Info của nút N> end; end; |
Trên đây là toàn bộ cách sử dụng cấu trúc cây mà bạn cần biết. Hy vọng bài viết của FUNiX hữu ích với bạn và hẹn gặp lại bạn trong các bài viết chia sẻ kiến thức lập trình tiếp theo!
Phạm Thị Thanh Ngọc









Bình luận (0
)