Giới thiệu về thuật toán Heap sort và ví dụ minh họa
Bài viết sau đây của FUNiX sẽ Giới thiệu về thuật toán Heap sort và ví dụ minh họa.
>> Khóa học Data Science Developer
>> Khóa học Phát triển ứng dụng Java Desktop
Thuật toán Heap Sort được dùng để sắp xếp dữ liệu đầu vào theo thứ tự tăng dần, xây dựng thành một heap tối đa.
1. Thuật toán Heap sort là gì?
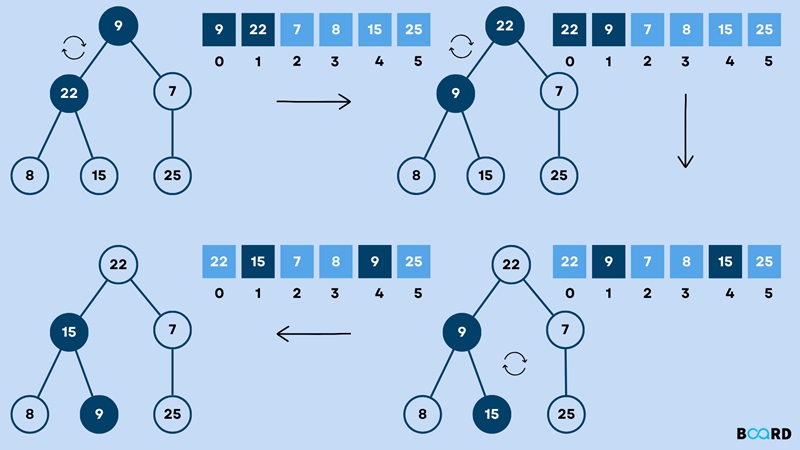

Thuật toán Heap sort là một kỹ thuật sắp xếp phân loại dựa trên cấu trúc dữ liệu Binary Heap. Heap sort giúp sắp xếp các phần tử trong danh sách sao cho phần tử lớn nhất được xếp vào cuối danh sách, và quá trình này sẽ lặp lại cho các phần tử còn lại trong danh sách.
Heap sort thường được người dùng lựa chọn sử dụng nhiều nhờ có tốc độ chạy nhanh và không quá phức tạp.
>>> Đọc ngay: Giới thiệu về cấu trúc Heap. Ví dụ minh họa
2. Cấu trúc dữ liệu Heap là gì?
Heap là cấu trúc dữ liệu đặc biệt dựa trên cấu trúc của một cây nhị phân hoàn chỉnh thỏa mãn thuộc tính heap, và có thể được biểu diễn dưới dạng một mảng. Một cây nhị phân sẽ có các mục được lưu trữ theo một thứ tự đặc biệt.
Thuật toán Heap sort sẽ được sử dụng để biểu diễn cho thuộc tính heap của một nút trong cây nhị phân, bao gồm 2 loại:
- Max heap: Phần tử trong nút cha luôn có giá trị lớn hơn so với tất cả các phần tử trong nút con. Và giá trị nút gốc là lớn nhất so với tất cả các nút khác.
- Min heap: Phần tử trong nút cha luôn có giá trị nhỏ hơn so với tất cả các phần tử trong nút con. Và giá trị nút gốc là nhỏ nhất so với tất cả các nút khác.
Ví dụ về cấu trúc dữ liệu Min Heap và Max Heap:
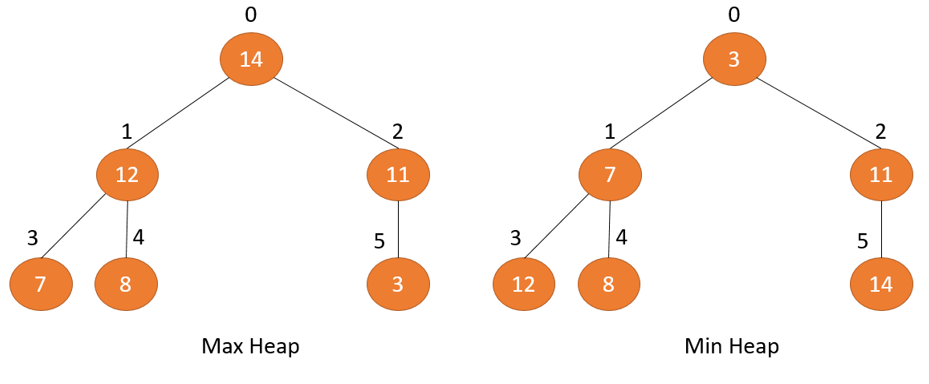

Thuật toán heap sort có thể được biểu diễn qua một cây hoặc mảng nhị phân.
>>> Đọc ngay: FUNiX – Học lấy bằng đại học trực tuyến giá trị ngang bằng đại học chính quy
3. Làm thế nào để tạo cấu trúc dữ liệu Heap cho một cây nhị phân
Một số thuật toán Heap sort được sử dụng để thực hiện những thao tác quan trọng trong cấu trúc Heap.
Chúng ta có thể sửa đổi một cây nhị phân hoàn chỉnh trở thành Max Heap bằng cách sử dụng hàm Heapify trên tất cả những phần tử không phải là nút lá của Heap. Ta sẽ xem ví dụ về tạo cấu trúc dữ liệu Heap cho một cây nhị phân với 3 phần tử:
heapify(array)
Root = array[0]
Largest = largest( array[0] , array [2*0 + 1]. array[2*0+2])
if(Root != Largest)
Swap(Root, Largest)
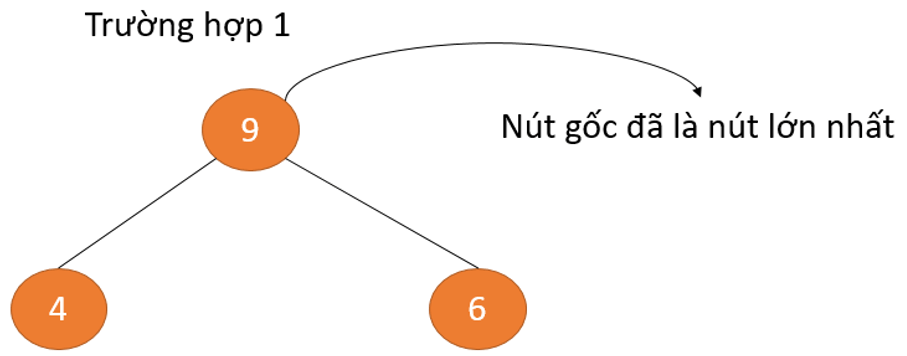

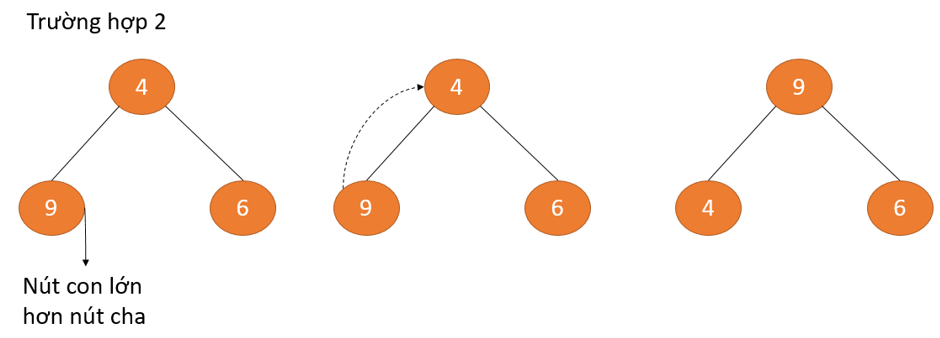

Trong trường hợp 1, nút gốc của cây nhị phân là phần tử lớn nhất và chúng ta không cần làm gì cả. Trường hợp 2, nút con chứa phần tử lớn hơn nút gốc, và ta cần hoán đổi để duy trì thuộc tính Max Heap.
Ví dụ 2:
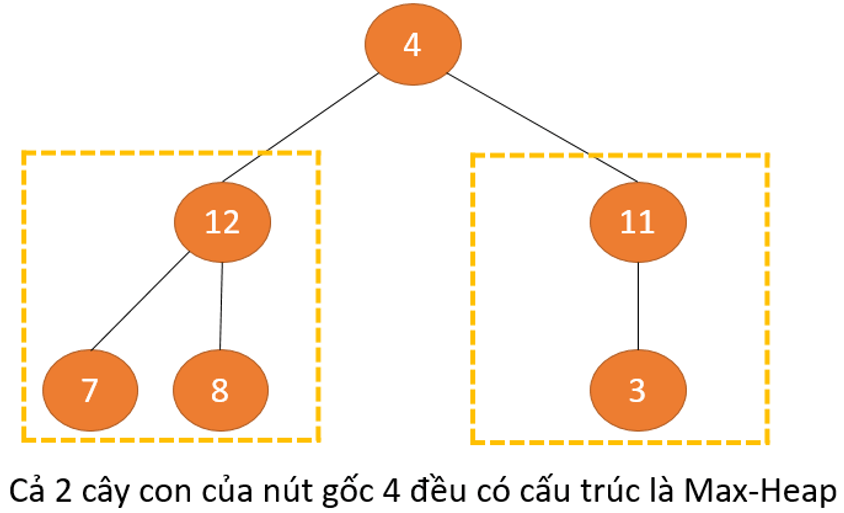

Trong ví dụ 2 này, cả 2 cây con đều có cấu trúc Max Heap, tuy nhiên nút gốc trên cùng lại không phải là Max Heap. Nên để duy trì thuộc tính Max Heap cho toàn bộ cây, chúng ta phải đẩy 2 cây xuống dưới cho đến khi đúng vị trí của nó.
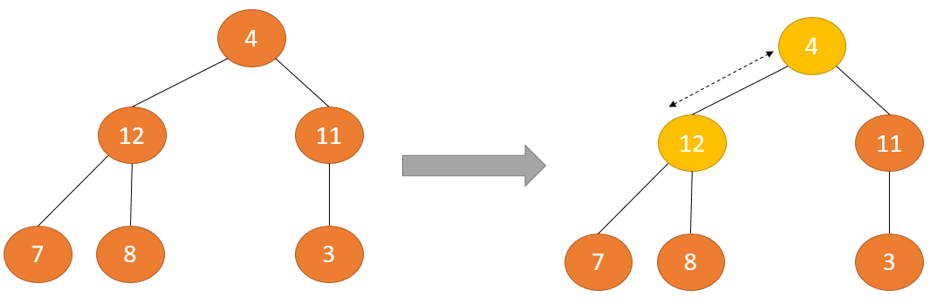

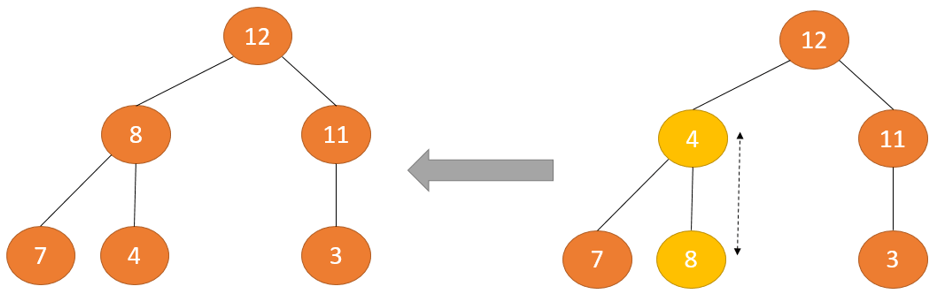

Trong một cây nhị phân có cả hai cây con đều là Max Heap, muốn duy trì thuộc tính Max Heap chúng ta cần phải thực hiện quá trình Heapify – tạo cấu trúc dữ liệu Heap từ cây nhị phân Binary Heap trên nút gốc nhiều lần cho đến khi nó lớn hơn tất cả các nút con.
Chúng ta có thể kết hợp 2 điều kiện này trong một hàm Heapify như sau:
void heapify(int arr[], int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
if (largest != i) {
swap(&arr[i], &arr[largest]);
heapify(arr, n, largest);
}
}
Chúng ta có thể di chuyển nút gốc đến vị trí chính xác để duy trì được thuộc tính Max Heap cho bất kỳ cây nhị phân nào miễn là cây con có cấu trúc Max Heap.
>>> Đọc ngay: Hướng dẫn sử dụng cấu trúc cây, cây tìm kiếm nhị phân
4. Hoạt động của thuật toán Heap sort
Thuật toán Heap sort sẽ hoạt động dựa trên các nguyên tắc sau:
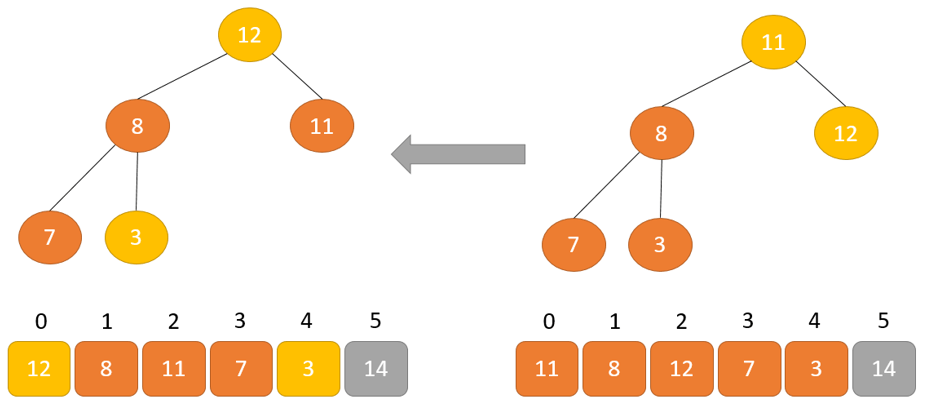
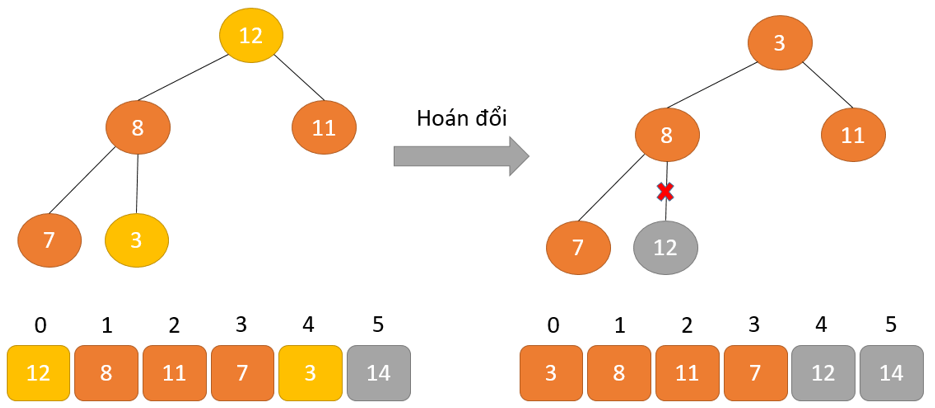
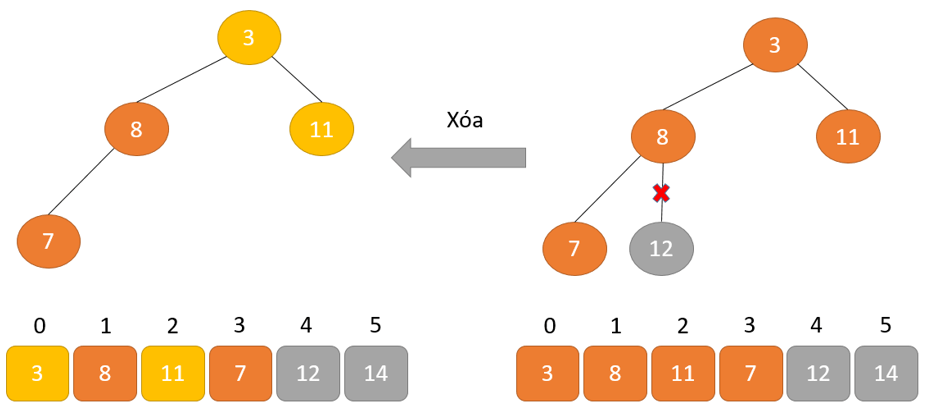
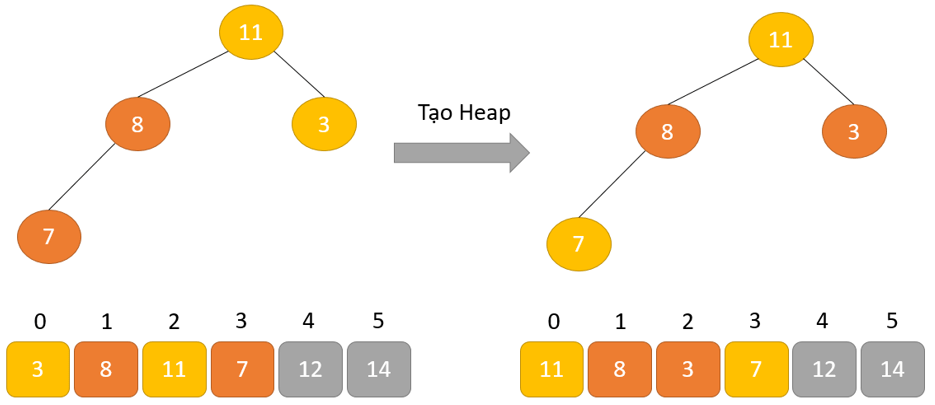
- Phần tử lớn nhất được đặt ở nút gốc theo thuộc tính Max Heap
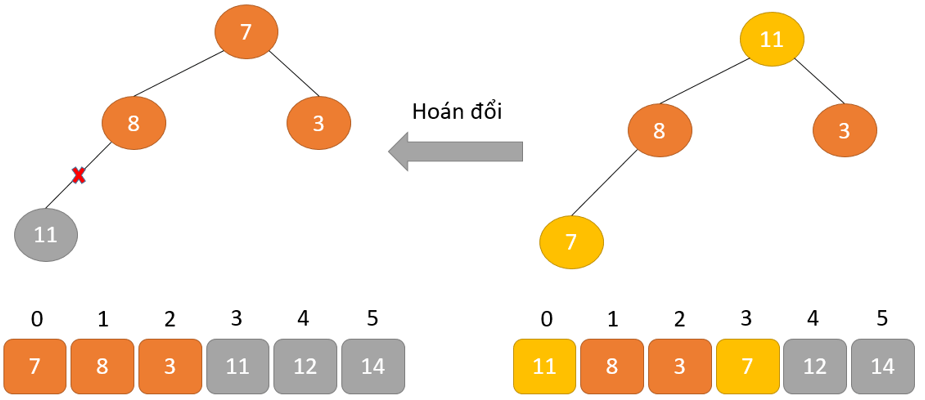
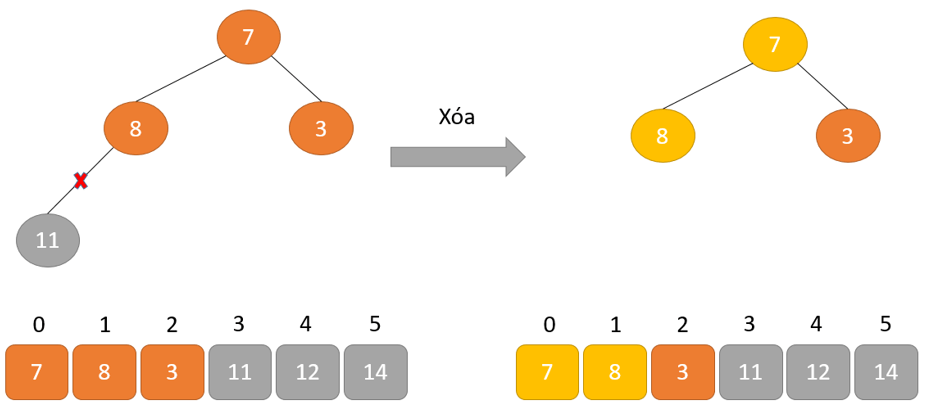
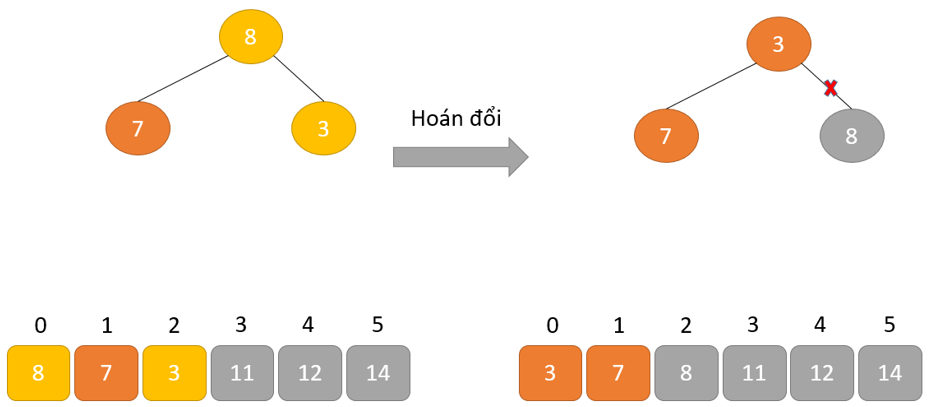
- Loại bỏ phần tử gốc và đặt nó ở cuối mảng nhị phân. Đặt phần tử cuối cùng của cây nhị phân vào chỗ trống.
- Giảm kích thước của Heap đi 1 đơn vị
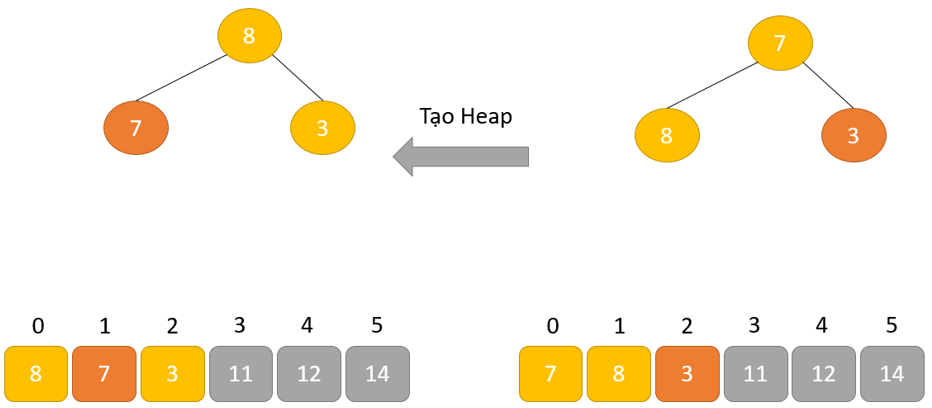
- Tạo cấu trúc dữ liệu Heap cho phần tử gốc để nút gốc chứa phần tử có giá trị lớn nhất.
- Lặp lại quá trình này cho đến khi tất cả các phần tử của danh sách được sắp xếp đúng.
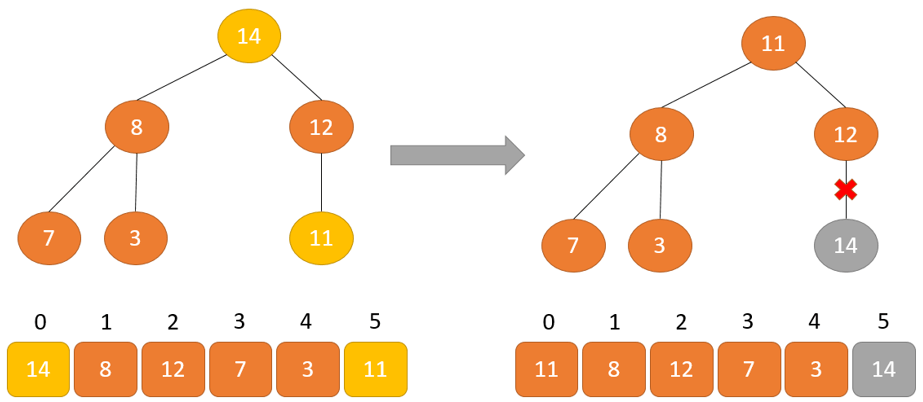









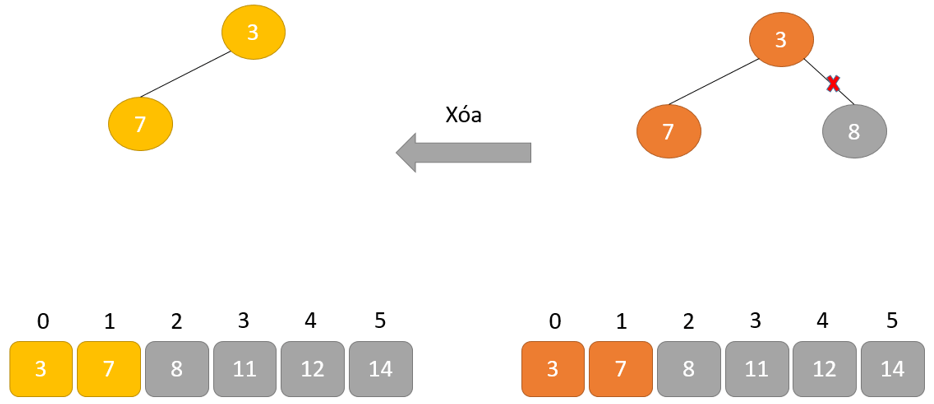

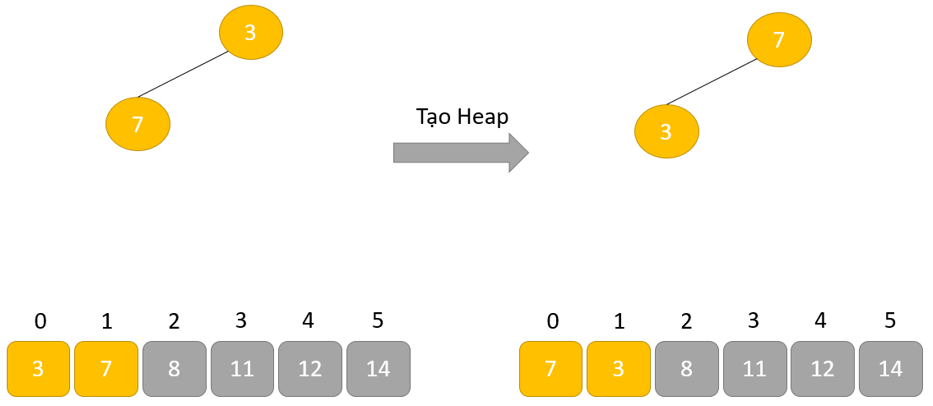

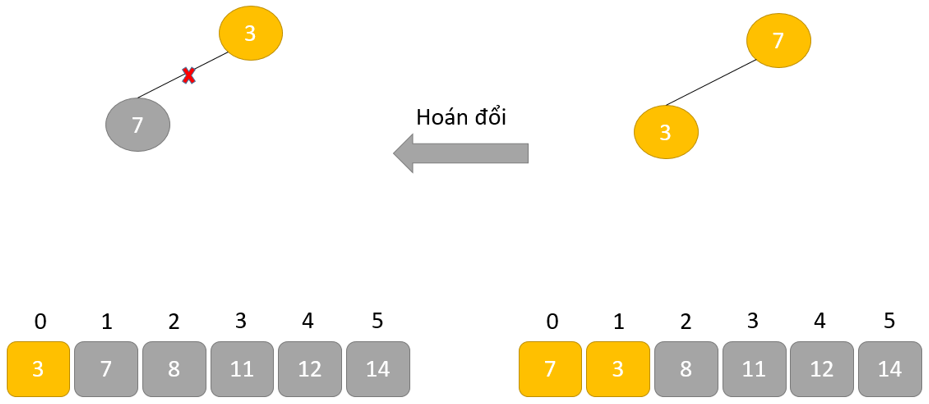

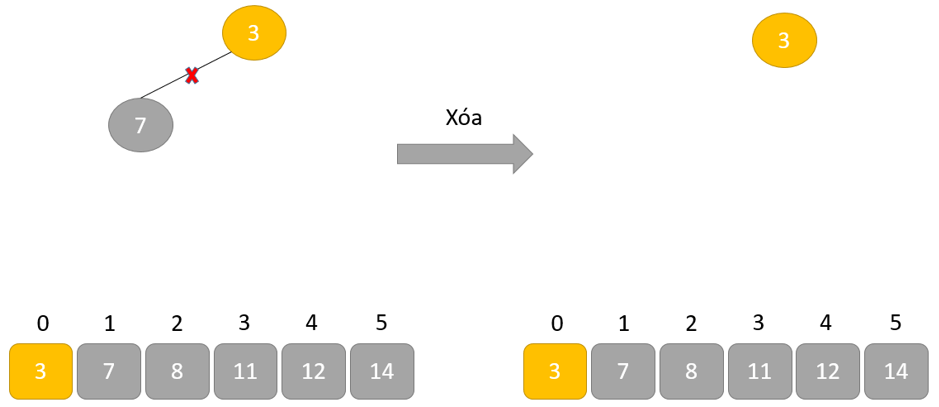

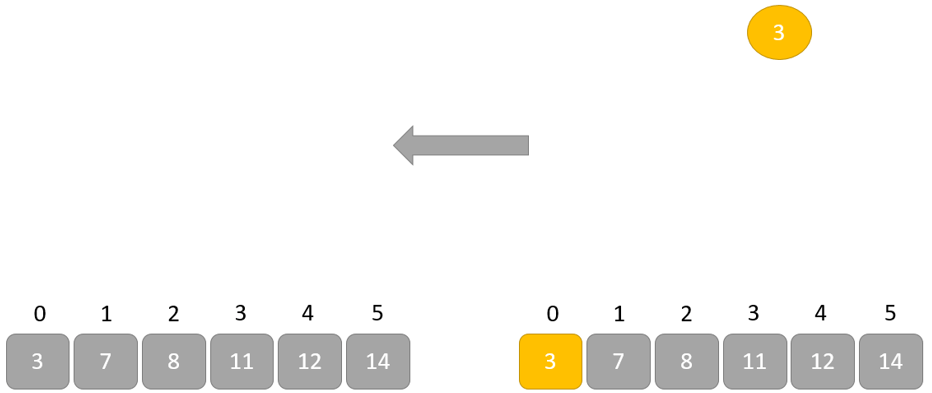

Cách hoạt động của Heap sort thể hiện trong đoạn mã dưới đây:
for (int i = n – 1; i >= 0; i–) {
swap(&arr[0], &arr[i]);
//Tạo cấu trúc heap cho phần tử gốc để lấy ra phần tử lớn nhất
heapify(arr, i, 0);
}
#include <stdio.h>
void swap(int *a, int *b) {
int c = *a;
*a = *b;
*b = c;
}
void heapify(int arr[], int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right; if (largest != i) {
swap(&arr[i], &arr[largest]);
heapify(arr, n, largest);
}
}
void sort_heap(int arr[], int n) {
for (int i = n / 2 – 1; i >= 0; i–)
heapify(arr, n, i);
for (int i = n – 1; i >= 0; i–) {
swap(&arr[0], &arr[i]);
heapify(arr, i, 0);
}
}
void print(int arr[], int n) {
for (int i = 0; i < n; ++i)
printf(“%d “, arr[i]);
printf(“\n”);
}
int main() {
int arr[] = {3, 14, 11, 7, 8, 12};
int n = sizeof(arr) / sizeof(arr[0]);
sort_heap(arr, n);
printf(“Mảng sau khi sắp xếp là: \n”);
print(arr, n); }
Kết quả nhận được:
Mảng sau khi sắp xếp là:
3 7 8 11 12 14
Trên đây là bài giới thiệu cơ bản của FUNiX về thuật toán Heap sort và ví dụ minh họa. Hy vọng các bạn có thể áp dụng vào trong chương trình của mình.
FUNiX là tổ chức giáo dục trực tuyến, đào tạo các khoá học Công nghệ thông tin từ cơ bản đến nâng cao với kiến thức được cập nhật mới nhất theo nhu cầu của người học: học để đi làm, học để lấy bằng đại học/chứng chỉ, học để nâng cao kiến thức trong lĩnh vực công nghệ thông tin.
Thành lập từ năm 2015, tính đến nay (tháng 4 năm 2023) đã có hơn 22.000 học viên đến từ các tỉnh thành tại Việt Nam và nhiều quốc gia trên thế giới theo học tại FUNiX.
>>> Nếu bạn đang có nhu cầu tìm hiểu về khóa học lập trình đi làm ngay. Hãy liên hệ với FUNiX ngay tại đây:


5 điều có thể bạn chưa biết về học lập trình trực tuyến FUNiX
Review khóa học trực tuyến FUNiX FPT đang được nhiều bạn trẻ lựa chọn
FUNiX đào tạo lập trình trực tuyến cung cấp nhân sự tập đoàn FPT
5 Điểm đáng chú ý tại khóa học lập trình trực tuyến FPT – FUNiX
Phạm Thị Thanh Ngọc









Bình luận (0
)